A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A
screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the
threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours.
On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws.
Formulate this problem as a LPP given that the objective is to maximize profit.
Let’s consider that the company manufactures x boxes of type A screws and y boxes of type B screws.
From the given information the below table is constructed:
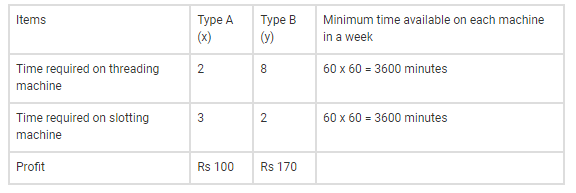
From the data in the above table, the objective function for maximum profit Z = 100x + 170y
Subject to the constraints
2x + 8y ≤ 3600 ⇒ x + 4y ≤ 1800 … (i)
3x + 2y ≤ 3600 … (ii)
x ≥ 0, y ≥ 0 (non-negative constraints)
Therefore, the required LPP is
Maximize: Z = 100x + 170y
Subject to constraints,
x + 4y ≤ 1800, 3x + 2y ≤ 3600, x ≥ 0, y ≥ 0.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.