A conical hole is drilled in a circular cylinder of height 12 cm

Given that:

$r=5 \mathrm{~cm}$

$h=12 \mathrm{~cm}$

We have the following diagram

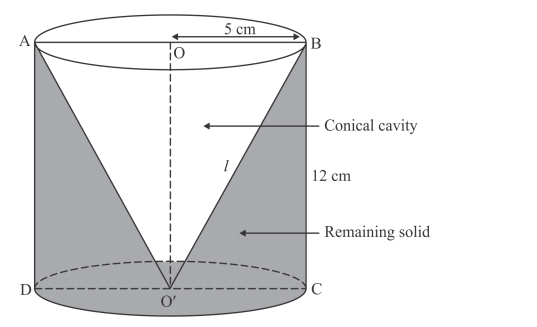
Slant height of cone is given by

$l=\sqrt{r^{2}+h^{2}}$

$=\sqrt{5^{2}+12^{2}}$

$=13 \mathrm{~cm}$

The total surface area of the remaining part is given by

$S=2 \pi r h+\pi r^{2}+\pi r l$

$=2 \times \pi \times 5 \times 12+\pi \times 5^{2}+\pi \times 5 \times 13$

$=120 \pi+25 \pi+65 \pi$

$=210 \pi \mathrm{cm}^{2}$

The volume of the remaining part is given by

$V=\pi r^{2} h-\frac{1}{3} \pi r^{2} h$

$=\frac{2}{3} \pi r^{2} h$

$=\frac{2}{3} \times \pi \times 5^{2} \times 12$

$=200 \pi \mathrm{cm}^{3}$

Hence, $S=210 \pi \mathrm{cm}^{2}, V=200 \pi \mathrm{cm}^{3}$