A conical vessel whose internal radius is 10 cm and height 48 cm

Solution:

Radius of conical vessel r = 10 cm

Height of conical vessel h = 48 cm

The volume of water = volume of conical vessel.

$=\frac{1}{3} \pi r^{2} h$

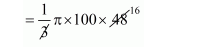
$=1600 \pi \mathrm{cm}^{3}$

$=1600 \times 3.14$

 

$=5024 \mathrm{~cm}^{3}$

Let h' be the height of cylindrical vessel, which filled by the water of conical vessel,

Radius of cylindrical vessel = 20 cm

Clearly,

Volume of cylindrical vessel = volume of water

$\pi \times(20)^{2} \times h=1600 \pi$

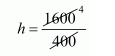
$h=4 \mathrm{~cm}$

Thus, the volume of the cylindrical vessel and height of cylindrical vessel are $5024 \mathrm{~cm}^{3}$ and $4 \mathrm{~cm}$ respectively.