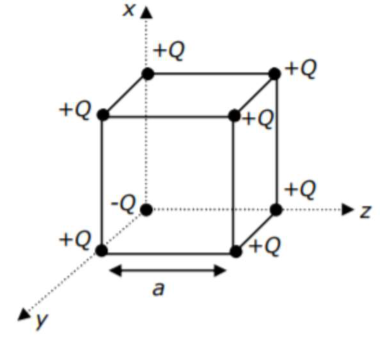
A cube of side ' $\mathrm{a}$ ' has point charges $+\mathrm{Q}$ located at each of its vertices except at the
origin where the charge is -Q. The electric field at the centre of cube is:
Correct Option: , 3
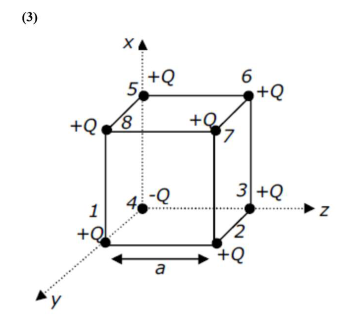
If only $+Q$ charges are placedat the corners of cube of side a then electric field at the centre of the cube will be zero.
But in the given condition one $(-Q)$ is placed at one corner of cube so here $\mathrm{E}_{1}=\mathrm{E}_{6}, \mathrm{E}_{2}=\mathrm{E}_{5}$ and $\mathrm{E}_{3}=\mathrm{E}_{8}$ (So it will cancel out each other so electric field at centre is due to
$\mathrm{Q}_{4}$ and $\mathrm{Q}_{7}$
Here electric field at centre $=2\left(\text { E. } f_{.}\right)_{4}$
As, $\left|\mathrm{E}_{4}\right|=\left|\mathrm{E}_{7}\right|$
$(E . F)_{C}=\frac{2 \mathrm{kQ}}{\left(\frac{\sqrt{3} \mathrm{a}}{2}\right)^{2}}=\frac{8 \mathrm{~K} Q}{3 \mathrm{a}^{2}} \quad\left\{\because \mathrm{K}=\frac{1}{4 \pi \varepsilon_{0}}\right\}$
$(E \cdot F)_{C}=\frac{2 Q}{3 a^{2} \pi \varepsilon_{0}}$
In vector form $\Rightarrow \vec{E}=\frac{-2 Q}{3 a^{2} \pi \varepsilon_{0}} \times\left(\frac{\hat{x}+\hat{y}+\hat{z}}{\sqrt{3}}\right)$
