Question:
A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is $5 \mathrm{~cm}$ and the angular speed of rotation is $\omega \mathrm{rad} \mathrm{s}^{-1}$. The difference in the height, $\mathrm{h}($ in $\mathrm{cm})$ of liquid at the centre of vessel and at the side will be:
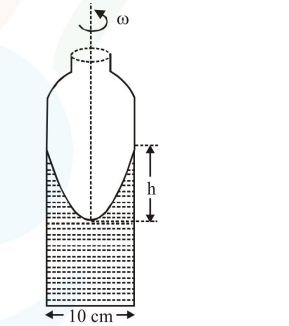
Correct Option: , 4
Solution:
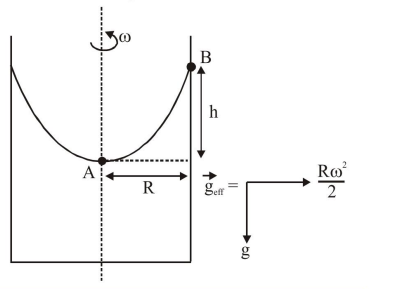
Applying pressure equation from A to B
$\mathrm{P}_{0}+\rho \cdot \frac{\mathrm{R} \omega^{2}}{2} \cdot \mathrm{R}-\rho g h=\mathrm{P}_{0}$
$\frac{\rho R^{2} \omega^{2}}{2}=\rho g h$
$\mathrm{h}=\frac{\mathrm{R}^{2} \omega^{2}}{2 \mathrm{~g}}=(5)^{2} \frac{\omega^{2}}{2 \mathrm{~g}}=\frac{25}{2} \frac{\omega^{2}}{\mathrm{~g}}$
