A floral design on a floor is made up of 16 tiles, each triangular in shape having sides 16 cm,

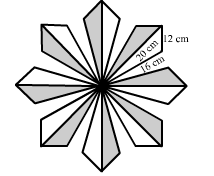
Area of one triangular-shaped tile can be found in the following manner:

Let :

$a=16 \mathrm{~cm}, b=12 \mathrm{~cm}$ and $c=20 \mathrm{~cm}$

$s=\frac{a+b+c}{2}=\frac{16+12+20}{2}=24 \mathrm{~cm}$

By Heron's formula, we have:

Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{24(24-16)(24-12)(24-20)}$

$=\sqrt{24 \times 8 \times 12 \times 4}$

$=\sqrt{6 \times 4 \times 4 \times 4 \times 4 \times 6}$

$=6 \times 4 \times 4$

$=96 \mathrm{~cm}^{2}$

Now,

Area of 16 triangular-shaped tiles $=16 \times 96=1536 \mathrm{~cm}^{2}$

Cost of polishing tiles of area $1 \mathrm{~cm}^{2}=$ Rs 1

Cost of polishing tiles of area $1536 \mathrm{~cm}^{2}=1 \times 1536=$ Rs 1536