Question:
A function $f$ is defined on $[-3,3]$ as
$f(x)=\left\{\begin{array}{cc}\min \left\{|x|, 2-x^{2}\right\}, & -2 \leq x \leq 2 \\ {[|x|]} & , 2<|x| \leq 3\end{array}\right.$
where $[\mathrm{x}]$ denotes the greatest integer $\leq \mathrm{x}$. The number of points, where $\mathrm{f}$ is not differentiable in $(-3,3)$ is
Solution:
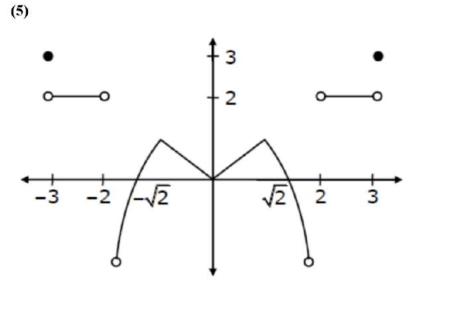
Points of non-differentiability in $(-3,3)$ are at $x=-2,-1,0,1,2$.
i.e. 5 points.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.