A line is a common tangent to the circle

Circle: $(x-3)^{2}+y^{2}=9$

Parabola: $y^{2}=4 x$

Let tangent $y=m x+\frac{a}{m}$

$y=m x+\frac{1}{m}$

$m^{2} x-m y+1=0$

the above line is also tangent to circle

$(x-3)^{2}+y^{2}=9$

$\therefore \perp$ from $(3,0)=3$

$\left|\frac{3 m^{2}-0+1}{\sqrt{m^{2}+m^{4}}}\right|=3$

$\left(3 m^{2}+1\right)^{2}=9\left(m^{2}+m^{4}\right)$

$6 m^{2}+1+9 m^{4}=9 m^{2}+9 m^{4}$

$3 m^{2}=1$

$m=\pm \frac{1}{\sqrt{3}}$

$\therefore$ tangent is

$y=\frac{1}{\sqrt{3}} x+\sqrt{3}$

or $\quad y=-\frac{1}{\sqrt{3}} x-\sqrt{3}$

(it will be used) (rejected)

$m=\frac{1}{\sqrt{3}}$

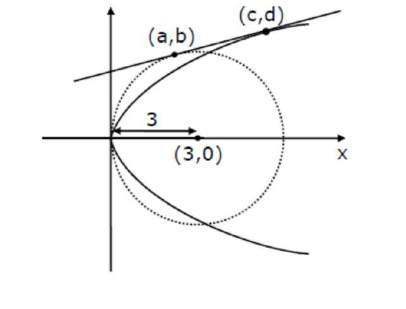
for Parabola $\left(\frac{a}{m^{2}}, \frac{2 a}{m}\right) \equiv(3,2 \sqrt{3})$

$(c, d)$

for Circle $\quad y=\frac{1}{r} x+\sqrt{3} \quad \& \quad(x-3)^{2}+y^{2}=9$

$y=\frac{1}{\sqrt{3}} x+\sqrt{3}$

solving, $(x-3)^{2}+\left(\frac{1}{\sqrt{3}} x+\sqrt{3}\right)^{2}=9$ mathB

$x^{2}+9-6 x+\frac{1}{3} x^{2}+3+2 x=9$

$\frac{4}{3} x^{2}-4 x+3=0$

$4 x^{2}-12 x+9=0$

$4 x^{2}-6 x-6 x+9=0$

$2 x(2 x-3)-3(2 x-3)=0$

$(2 x-3)(2 x-3)=0$

$x=\frac{3}{2}$

$\therefore \quad y=\frac{1}{\sqrt{3}}\left(\frac{3}{2}\right)+\sqrt{3}$

$(a, b) \equiv\left(\frac{3}{2}, \frac{3 \sqrt{3}}{2}\right)$

$y=\frac{3 \sqrt{3}}{2}$

$2(a+c)=2\left(\frac{3}{2}+3\right)$

$=2\left(\frac{3}{2}+\frac{6}{2}\right)$

$=9$