Question:
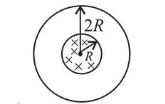
A long solenoid of radius $R$ carries a time $(t)$ - dependent current $I(t)=I_{0} t(1-t)$. A ring of radius $2 R$ is placed coaxially near its middle. During the time interval $0 \leq t \leq$ 1 , the induced current $\left(I_{R}\right)$ and the induced $\operatorname{EMF}\left(V_{R}\right)$ in the ring change as:
Correct Option: , 4
Solution:
(4) According to question, $I(t)=I_{0} t(1-t)$
$\therefore I=\mathrm{I}_{0} \mathrm{t}-I_{0} t^{2}$
$\phi=B \cdot A$
$\phi=\left(\mu_{0} n I\right) \times\left(\pi \mathrm{R}^{2}\right)$
$\left(\because B=\mu_{0} \mathrm{nI}\right.$ and $\left.A=\pi R^{2}\right)$
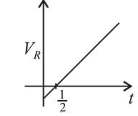
$V_{R}=\frac{-\mathrm{d} \phi}{d t}$
$V_{R}=\mu_{0} n \pi R^{2}\left(I_{0}-2 I_{0} t\right)$
$\Rightarrow V_{R}=0$ at $t=\frac{1}{2} s$