A long, straight wire of radius a carries a current distributed uniformly over its cross-section. The ratio of the magnetic

(1) Let $a$ be the radius of the wire

Magnetic field at point $A$ (inside)

$B_{A}=\frac{\mu_{0} i r}{2 \pi a^{2}}=\frac{\mu_{0} i \frac{a}{3}}{2 \pi a^{2}}=\frac{\mu_{0} i}{\pi a^{2}} \frac{a}{6}=\frac{\mu_{0} i}{6 \pi a}$

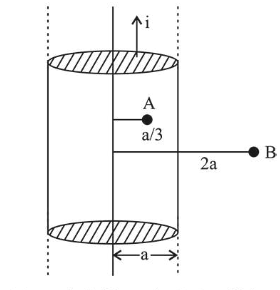
Magnetic field at point B (outside)

$B_{B}=\frac{\mu_{0} i}{2 \pi(2 a)}$

$\therefore \quad \frac{B_{A}}{B_{B}}=\frac{\frac{\mu_{0} i}{6 \pi a}}{\frac{\mu_{0} i}{2 \pi(2 \mathrm{a})}}=\frac{4}{6}=\frac{2}{3}$