A metallic right circular cone 20 cm high

We have the following situation

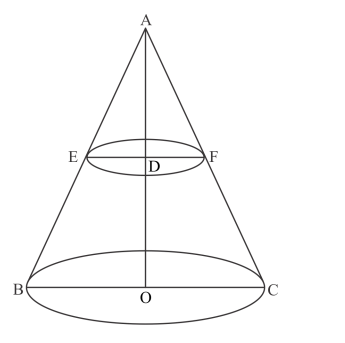
Let ABC be the cone. The height of the metallic cone is AO=20cm. The cone is cut into two parts at the middle point of its axis. Hence, the height of the

frustum cone is AD=10cm. Since, the angle A is right angled, so each of the angles B and C are 45 degrees. Also, the angles E and F each are equal to 45

degrees. Let the radii of the top and bottom circles of the frustum cone are r1 cm and r2 cm respectively.

From the triangle ADE, we have

$\frac{\mathrm{DE}}{\mathrm{AD}}=\cot 45^{\circ}$

$\Rightarrow \frac{r_{1}}{10}=1$

$\Rightarrow r_{1}=10 \mathrm{~cm}$

From the triangle AOB, we have

$\frac{\mathrm{OB}}{\mathrm{OA}}=\cot 45^{\circ}$

$\Rightarrow \frac{r_{2}}{20}=1$

$\Rightarrow r_{2}=20 \mathrm{~cm}$

The volume of the frustum cone is

$V=\frac{1}{3} \pi\left(r_{1}^{2}+r_{1} r_{2}+r_{2}^{2}\right) \times h$

$=\frac{1}{3} \pi\left(10^{2}+10 \times 20+20^{2}\right) \times 10$

$=\frac{1}{3} \times \frac{22}{7} \times 700 \times 10$

$=\frac{22000}{3} \mathrm{~cm}^{3}$

The radius of the wire is $\frac{1}{32} \mathrm{~cm}$. Let the length of the wire be $/ \mathrm{cm}$. Then, the volume of the wire is

$V_{1}=\pi\left(\frac{1}{32}\right)^{2} \times l \mathrm{~cm}^{3}$

Since, the frustum is drawn in the wire, their volumes must be equal. Hence, we have

$V_{1}=V$

$\Rightarrow \pi\left(\frac{1}{32}\right)^{2} \times l=\frac{22000}{3}$

$\Rightarrow \quad l=\frac{22000 \times(32)^{2} \times 7}{3 \times 22}$

$\Rightarrow \quad l=\frac{1000 \times(32)^{2} \times 7}{3}$

$\Rightarrow \quad l=2389333.33 \mathrm{~cm}$

$\Rightarrow \quad l=23893.33 \mathrm{~m}$

Hence, the length of the wire is 23893.33 m.