A number is chosen from the numbers 1 to 100.

let A denote the event that the number is divisible by 4 and B denote the event that the number is divisible by 4.

To find : Probability that the number is both divisible by 4 or $6=P(A$ or $B)$

The formula used : Probability =

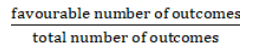
$P(A$ or $B)=P(A)+P(B)-P(A$ and $B)$

Numbers from 1 to 100 divisible by 4 are $4,8,12,16,20,24,28,32,36,40,44,48,52$, $56,60,64,68,72,76,80,84,88,92,96,100$.

There are 25 numbers from 1 to 100 divisible by 4

Favourable number of outcomes $=25$

Total number of outcomes $=100$ as there are 100 numbers from 1 to 100

$P(A)=\frac{25}{100}$

Numbers from 1 to 100 divisible by 6 are 6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96

There are 16 numbers from 1 to 100 divisible by 6

Favourable number of outcomes $=16$

Total number of outcomes $=100$ as there are 100 numbers from 1 to 100

$P(B)=\frac{16}{100}$

Numbers from 1 to 100 divisible by both 4 and 6 are

$12,24,36,48,60,72,84,96$

There are 8 numbers from 1 to 100 divisible by both 4 and 6 Favourable number of outcomes $=8$

$P(A$ and $B)=\frac{8}{100}$

$\mathrm{P}(\mathrm{A}$ or $\mathrm{B})=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})-\mathrm{P}(\mathrm{A}$ and $\mathrm{B})$

$P(A$ or $B)=\frac{25}{100}+\frac{16}{100}-\frac{8}{100}$

$P(A$ or $B)=\frac{25+16-8}{100}=\frac{33}{100}$

$P(A$ or $B)=\frac{33}{100}$

The probability that the number is both divisible by 4 or $6=P(A$ or $B)=\frac{33}{100}$