A parallel plate capacitor has plate of length ' l ', width ' w ' and separation of plates is ' d '.

(2) Capacitance before inserting the slab,

$C_{i}=\frac{\varepsilon_{0} A}{d}=\frac{\varepsilon_{0} l w}{d}$                          $(\because A=l w)$

Capacitance after inserting the dielectric slab,

$C_{f}=\frac{K \varepsilon_{0} A_{1}}{d}+\frac{\varepsilon_{0} A_{2}}{d}$

$=\frac{K \varepsilon_{0} W x}{d}+\frac{\varepsilon_{0} w(l-x)}{d}$

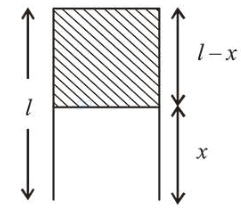
According to question,

$2 \times$ Initial energy $=$ Final energy

$\Rightarrow\left(\frac{1}{2} C_{i} V^{2}\right) 2=\frac{1}{2} C_{f} V^{2}$

$\Rightarrow 2 C_{i}=C_{f}$

$\Rightarrow 2\left(\frac{\varepsilon_{0} w l}{d}\right)=\frac{\varepsilon_{0} K w x}{d}+\frac{\varepsilon_{0} w(l-x)}{d}$

$\Rightarrow 2 l=k x+(l-x) \Rightarrow x=\frac{l}{3}$