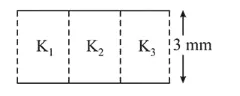
A parallel plate capacitor is of area $6 \mathrm{~cm}^{2}$ and a separation $3 \mathrm{~mm}$. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constants $\mathrm{K}_{1}=10, \mathrm{~K}_{2}=12$ and $\mathrm{K}_{3}=1(4)$ The dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be:
Correct Option: , 3
(3) Let dielectric constant of material used be $\mathrm{K}$.
$\frac{k_{1} \epsilon_{0} A_{1}}{d}+\frac{k_{2} \epsilon_{0} A_{2}}{d}+\frac{k_{3} \epsilon_{0} A_{3}}{d}=\frac{k \in_{0} A}{d}$
or
$\frac{10 \in_{0} \mathrm{~A} / 3}{\mathrm{~d}}+\frac{12 \epsilon_{0} \mathrm{~A} / 3}{\mathrm{~d}}+\frac{14 \in_{0} \mathrm{~A} / 3}{\mathrm{~d}}=\frac{\mathrm{K} \in_{0} \mathrm{~A}}{\mathrm{~d}}$
$\frac{\epsilon_{0} \mathrm{~A}}{\mathrm{~d}}\left(\frac{10}{3}+\frac{12}{3}+\frac{14}{3}\right)=\frac{\mathrm{K} \epsilon_{0} \mathrm{~A}}{\mathrm{~d}}$
$\therefore \mathrm{K}=12$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.