A parallel plate capacitor with square plates is filled with four dielectrics of dielectric constants
A parallel plate capacitor with square plates is filled with four dielectrics of dielectric constants $\mathrm{K}_{1}, \mathrm{~K}_{2}, \mathrm{~K}_{3}, \mathrm{~K}_{4}$ arranged as shown in the figure. The effective dielectric constant $\mathrm{K}$ will be:
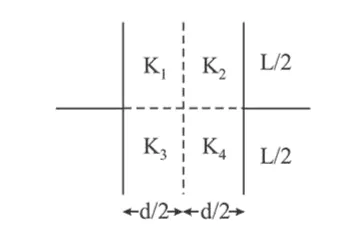
Correct Option: , 4
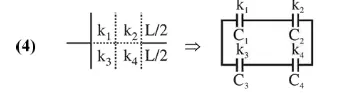
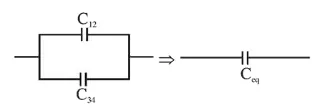
$C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}=\frac{\frac{k_{1} \in_{0} \frac{L}{2} \times L}{d / 2} \cdot \frac{k_{2}\left[\epsilon_{0} \frac{L}{2} \times L\right]}{d / 2}}{\left(k_{1}+k_{2}\right)\left[\frac{\epsilon_{0} \frac{L}{2} \times L}{d / 2}\right]}$
$\mathrm{C}_{12}=\frac{\mathrm{k}_{1} \mathrm{k}_{2}}{\mathrm{k}_{1}+\mathrm{k}_{2}} \frac{\in_{0} \mathrm{~L}^{2}}{\mathrm{~d}}$
in the same way we get,
$C_{34}=\frac{k_{3} k_{4}}{k_{3}+k_{4}} \frac{\epsilon_{0} L^{2}}{d}$
$\therefore C_{e q}=C_{12}+C_{34}=\left[\frac{k_{1} k_{2}}{k_{1}+k_{2}}+\frac{k_{3} k_{4}}{k_{3}+k_{4}}\right] \frac{\epsilon_{0} L^{2}}{d}$ ....(1)
Now if $k_{e q}=K, C_{e q}=\frac{k \in_{0} L^{2}}{d}$ ....(2)
on comparing equation (i) to equation (ii), we get
$\mathrm{k}_{\mathrm{eq}}=\frac{\mathrm{k}_{1} \mathrm{k}_{2}\left(\mathrm{k}_{3}+\mathrm{k}_{4}\right)+\mathrm{k}_{3} \mathrm{k}_{4}\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)}{\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)\left(\mathrm{k}_{3}+\mathrm{k}_{4}\right)}$
