A particle is moving unidirectionally on a horizontal plane under the action of a constant power supplying energy source.
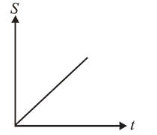
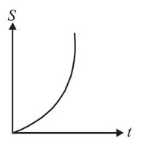
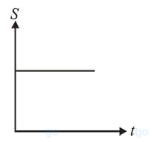
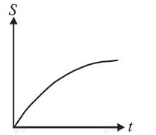
A particle is moving unidirectionally on a horizontal plane under the action of a constant power supplying energy source. The displacement $(s)$ - time $(t)$ graph that describes the motion of the particle is (graphs are drawn schematically and are not to scale) :
Correct Option: , 2
(2) We know that
Power, $P=F v$
But $F=m a v=m \frac{d v}{d t} v$
$\therefore P=m v \frac{d v}{d t} \Rightarrow P d t=m v d v$
Integrating both sides $\int_{0}^{t} P d t=m \int_{0}^{v} v d v$
P. $\mathrm{t}=\frac{1}{2} m v^{2} \Rightarrow v=\left(\sqrt{\frac{2 P}{m}}\right) t^{1 / 2}$
Distance, $s=\int_{0}^{t} v d t=\sqrt{\frac{2 P}{m}} \int_{0}^{t} t^{1 / 2} d t=\sqrt{\frac{2 P}{m}} \cdot \frac{t^{3 / 2}}{3 / 2}$
$\Rightarrow s=\sqrt{\frac{8 P}{9 m}} \cdot t^{3 / 2} \Rightarrow \mathrm{s} \propto \mathrm{t}^{3 / 2}$