A particle of mass

Question:
A particle of mass $1 \mathrm{~kg}$ is hanging from a spring of force constant $100 \mathrm{Nm}^{-1}$. The mass is pulled slightly downward and released so that it executes free simple harmonic motion with time period $\mathrm{T}$. The time when the kinetic energy and potential

The time when the kinetic energy and potential energy of the system will become equal, is $\frac{T}{x}$. The value of $x$ is_______.

Solution:

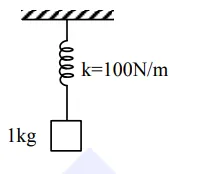
$\mathrm{KE}=\mathrm{PE}$

$\mathrm{y}=\frac{\mathrm{A}}{\sqrt{2}}=\mathrm{A} \sin \omega \mathrm{t}$

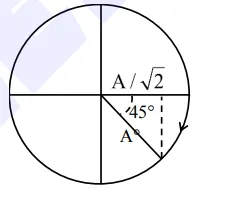
$\mathrm{t}=\frac{\mathrm{T}}{8}=\frac{\mathrm{T}}{\mathrm{x}}$

$x=8$

A particle of mass

Leave a comment

All Study Material