A particle of mass $200 \mathrm{MeV} / \mathrm{c}^{2}$ collides with a hydrogen atom at rest. Soon after the collision the particle comes to rest, and the atom recoils and goes to its first excited state. The initial kinetic energy of the particle (in eV) is
$\frac{\mathrm{N}}{4}$ The value of $\mathrm{N}$ is
(Given the mass of the hydrogen atom to be $1 \mathrm{GeV} / \mathrm{c}^{2}$ )
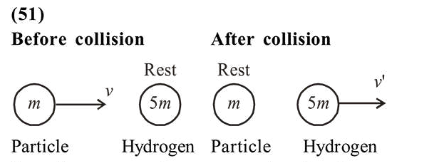
From linear momentum conservation, $L_{i}=L_{f}$
$m V+0=0+5 m V^{\prime} \Rightarrow V^{\prime}=\frac{v}{5}$
Loss of $K E=K E_{i}-K E_{f}=\frac{1}{2} m v^{2}-\frac{1}{2}(5 m)\left(\frac{v}{5}\right)^{2}$
$=\frac{1}{2} m v^{2}\left(1-\frac{1}{5}\right)=\frac{4}{5}\left(\frac{m v^{2}}{2}\right)$
$=\frac{4}{5} K E_{i}=10.2 \mathrm{eV}$
$[\because$ Energy in first excited state of atom $=10.2 \mathrm{eV}]$
$K E_{i}=12.75 \mathrm{eV}=\frac{\mathrm{N}}{4} \Rightarrow N=51$
The value of $N=51$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.