Question:
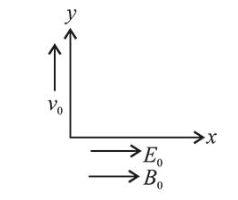
A particle of mass $m$ and charge $q$ has an initial velocity
$\vec{v}=v_{0} \hat{j}$. If an electric field $\vec{E}=E_{0} \vec{i}$ and magnetic field
$\vec{B}=B_{0} \hat{i}$ act on the particle, its speed will double after a time:
Correct Option: , 3
Solution:
(3) In the $x$ direction
$F_{x}=q E$
$\Rightarrow \quad m a_{x}=q E$
$\Rightarrow \quad a_{x}=\frac{E_{0} q}{m}$
For speed to be double,
$v_{0}^{2}+v_{x}^{2}=\left(2 v_{0}\right)^{2}$
$\Rightarrow v_{x}=\sqrt{3} v_{0}=a_{x} t$
$\Rightarrow \sqrt{3} v_{0}=0+\frac{q E_{0} t}{m} \Rightarrow t=\frac{\sqrt{3} v_{0} m}{E_{0} q}$