A particle of mass $m$ is dropped from a height $h$ above the ground. At the same time another particle of the same mass is thrown vertically upwards from the ground with a speed of $\sqrt{2 g h}$. If they collide head-on completely inelastically, the time taken for the combined mass to reach the ground, in units of $\sqrt{\frac{h}{g}}$ is:
Correct Option: , 4
(4)
Let 1 ve ue ume taken uy me parucie uroppea нom height $\mathrm{h}$ to collide with particle thrown upward.
Using,
$v^{2}-u^{2}=2 g h$
$\Rightarrow v^{2}-0^{2}=2 g h$
$\Rightarrow v=\sqrt{2 g h}$
Downward distance travelled
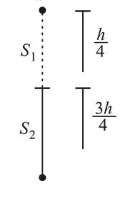
$S_{1}=\frac{1}{2} g t^{2}=\frac{1}{2} g \cdot \frac{h}{2 g}=\frac{h}{4}$
Distance of collision point from ground
$s_{2}=h-\frac{h}{4}=\frac{3 h}{4}$
Speed of (A) just before collision
$v_{1}=g t=\sqrt{\frac{g h}{2}}$
And speed of(B) just before collision
$v_{2}=\sqrt{2 g h}-\sqrt{\frac{g h}{2}}$
Using principle of conservation of linear momentum
$m v_{1}+m v_{2}=2 m v_{f}$
$\frac{\Rightarrow v_{f}=m\left(\sqrt{2 g h}-\sqrt{\frac{g h}{2}}\right)-m \sqrt{\frac{g h}{2}}=0}{2 m}$
After collision, time taken $\left(t_{1}\right)$ for combined mass to reach the ground is
$\Rightarrow \frac{3 h}{4}=\frac{1}{2} g t_{1}^{2}$
$\Rightarrow t_{1}=\sqrt{\frac{3 h}{2 g}}$
