A passenger train takes 3 hours less for a journey of 360 km,

Let the usual speed of train be $x \mathrm{~km} / \mathrm{hr}$ then,

Increased speed of the train $=(x+10) \mathrm{km} / \mathrm{hr}$

Time taken by the train under usual speed to cover $360 \mathrm{~km}=\frac{360}{x} \mathrm{hr}$

Time taken by the train under increased speed to cover $360 \mathrm{~km}=\frac{360}{(x+10)} \mathrm{hr}$

Therefore,

$\frac{360}{x}-\frac{360}{(x+10)}=3$

$\frac{\{360(x+10)-360 x\}}{x(x+10)}=3$

$\frac{360 x+3600-360 x}{x^{2}+10 x}=3$

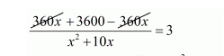
$3600=3 x^{2}+30 x$

$3 x^{2}+30 x-3600=0$

$3\left(x^{2}+10 x-1200\right)=0$

$x^{2}+10 x-1200=0$

$x^{2}-30 x+40 x-1200=0$

$x(x-30)+40(x-30)=0$

$(x-30)(x+40)=0$

So, either 

$(x-30)=0$

$x=30$

Or

$(x+40)=0$

$x=-40$

But, the speed of the train can never be negative.

Hence, the usual speed of train is $x=30 \mathrm{~km} / \mathrm{hr}$