Question:
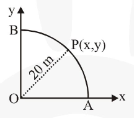
A point $P$ moves in counter clockwise direction on a circular path as shown in the figure. The movement of ' $\mathrm{P}^{\prime}$ is such that it sweeps out a length $\mathrm{s}=\mathrm{t}^{3}+5$, where $\mathrm{s}$ is in metres and $\mathrm{t}$ is in seconds. The radius of the path is $20 \mathrm{~m}$. The acceleration of ' $P^{\prime}$ when $t=2 \mathrm{~s}$ is nearly :
Correct Option: 1
Solution:

