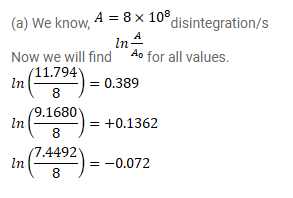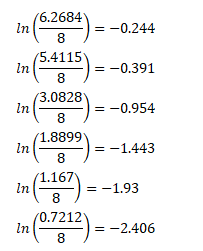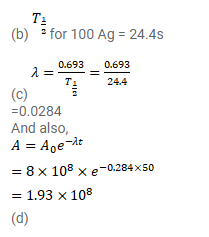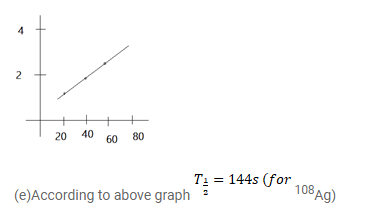A sample contains a mixture of ${ }^{108} \mathrm{Ag}$ and ${ }^{110} \mathrm{Ag}$ isotopes each having an activity of $8.0 \times 10^{8}$ disintegrations per second. ${ }^{110} \mathrm{Ag}$ is known to have a larger half-life than ${ }^{108} \mathrm{Ag}$. The activity $\mathrm{A}$ is measured as a function of time and the following data are obtained.
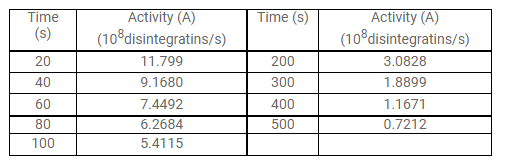
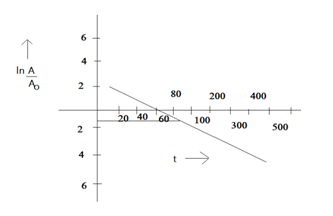
(a) Plot In $\left(\mathrm{A} / \mathrm{A}_{0}\right)$ versus time.
(b) See that for large values of time, the plot is nearly linear. Deduce the half-life of 110 Ag from this portion of the plot.
(c) Use the half-life of ${ }^{110} \mathrm{Ag}$ to calculate the activity corresponding to ${ }^{106} \mathrm{Ag}$ in the first $50 \mathrm{~s}$.
(d) Plot In $\left(\mathrm{A} / \mathrm{A}_{0}\right)$ versus time for ${ }^{108} \mathrm{Ag}$ for the first $50 \mathrm{~s}$.
(e) Find the half-life of ${ }^{108} \mathrm{Ag}$.