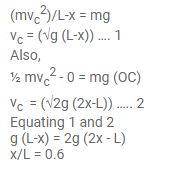A simple pendulum of length $L$ having a bob of mass $m$ is deflected from its rest position by an angle 9 and released (figure 8-E16). The string hits a peg which is fixed at a distance $x$ below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with $\theta=90^{\circ}$ and $x=L / 2$ find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of $x / L$ for which the bob goes in a complete circle about the peg when the pendulum is released from $\theta=90^{\circ}$.
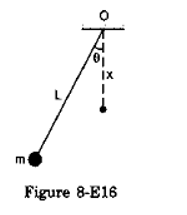
Total energy at A and B are same
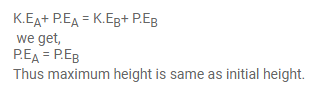
(b)
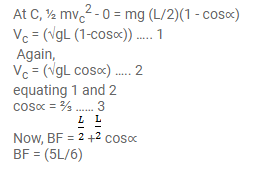
(c)