Question:
A solid sphere of radius $\mathbf{R}$ gravitationally attracts a particle placed at $3 \mathbf{R}$ from its centre with a force $\mathrm{F}_{1}$. Now a spherical cavity of radius $\left(\frac{\mathrm{R}}{2}\right)$ is made in the sphere (as shown in figure) and the force becomes $\mathrm{F}_{2}$. The value of $\mathrm{F}_{1}: \mathrm{F}_{2}$ is :
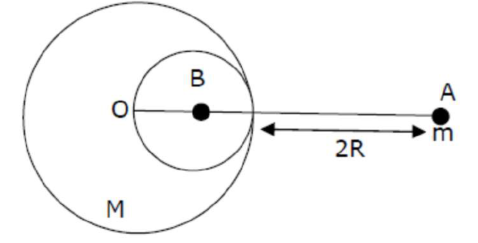
Correct Option: 1
Solution:
(1)
$g_{1}=\frac{G M}{(3 R)^{2}}=\frac{G M}{9 R^{2}}$
$g_{2}=\frac{G M}{9 R^{2}}-\frac{G\left(\frac{M}{8}\right)}{\left(3 R-\frac{R}{2}\right)^{2}}$
$=\frac{G M}{9 R^{2}}-\frac{G M}{R^{2} 50}=\frac{41}{9 \times 50} \frac{G M}{R^{2}}$
$\frac{g_{1}}{g_{2}}=\frac{41}{50}$
Force $\Rightarrow \frac{F_{1}}{F_{2}}=\frac{m g_{1}}{m g_{2}}=\frac{41}{50}$
