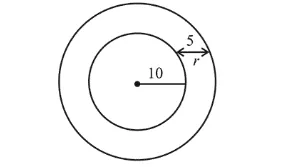
A spherical iron ball of radius $10 \mathrm{~cm}$ is coated with a layer of ice of uniform thickness that melts at a rate of $50 \mathrm{~cm}^{3} / \mathrm{min}$. When the thickness of the ice is $5 \mathrm{~cm}$, then the rate at which the thickness (in $\mathrm{cm} / \mathrm{min}$ ) of the ice decreases, is :
Correct Option: 1
(1) Given that ice melts at a rate of $50 \mathrm{~cm}^{3} / \mathrm{min}$.
$\therefore \frac{d V_{\text {ice }}}{d t}=50$
$V_{\text {ice }}=\frac{4}{3} \pi(10+r)^{3}-\frac{4}{3} \pi(10)^{3}$
$\Rightarrow \frac{d V}{d t}=\frac{4}{3} \pi 3(10+r)^{2} \frac{d r}{d t}=4 \pi(10+r)^{2} \frac{d r}{d t}$
Substitute $r=5$,
$50=4 \pi(225) \frac{d r}{d t} \Rightarrow \frac{d r}{d t}=\frac{50}{4 \pi(225)}=\frac{1}{18 \pi} \mathrm{cm} / \mathrm{min}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.