Question:
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
Solution:
External radius of spherical shell
$r_{1}=\frac{18}{2}=9 \mathrm{~cm}$
Let r2 be the internal radius of spherical shell.
Height of right circular cylinder h = 8 cm
& radius of right circular cylinder
$r=\frac{12}{2}=6 \mathrm{~cm}$
Clearly, volume of spherical shell = volume of right circular cylinder
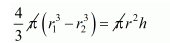
$\frac{4}{3}\left(9^{3}-r_{2}^{3}\right)=(6)^{2} \times 8$
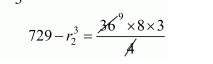
$729-r_{2}^{3}=216$
$r_{2}^{3}=513$
$r_{2}=\sqrt[3]{513}$
$r_{2}=3(19)^{1 / 3} \mathrm{~cm}$
