A spring mass system (mass m, spring constant k and natural length l ) rests in equilibrium on a horizontal disc.
Question:
A spring mass system (mass $m$, spring constant $k$ and natural length $l$ ) rests in equilibrium on a horizontal disc. The free end of the spring is fixed at the centre of the disc. If the disc together with spring mass system, rotates about it's axis with an angular velocity $\omega,\left(k>>m \omega^{2}\right)$ the relative change in the length of the spring is best given by the option:
Correct Option: , 3
Solution:
(3) Free body diagram in the frame of disc
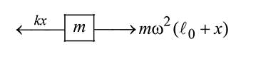
$\therefore m \omega^{2}\left(\ell_{0}+x\right)=k x$
$\Rightarrow x=\frac{m \ell_{0} \omega^{2}}{k-m \omega^{2}}$
For $k \gg m \omega^{2}$
$\Rightarrow \frac{x}{\ell_{0}}=\frac{m \omega^{2}}{k}$
