Question:
A square is inscribed in the circle $x^{2}+y^{2}-6 x+8 y-103=0$ with its sides parallel to the coordinate axes. Then the distance of the vertex of this square which is nearest to the origin is :
Correct Option: , 3
Solution:
The equation of circle is,
$x^{2}+y^{2}-6 x+8 y-103=0$
$\Rightarrow \quad(x-3)^{2}+(y+4)^{2}=(8 \sqrt{2})^{2}$
$C(3,-4), r=8 \sqrt{2}$
$\Rightarrow \quad$ Length of side of square $=\sqrt{2} r=16$
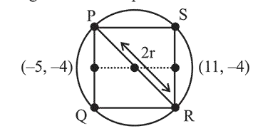
$\Rightarrow \quad P(-5,4), Q(-5,-12)$
$R(11,-12), S(11,4)$
$\Rightarrow \quad$ Required distance $=O P$
$=\sqrt{(-5-0)^{2}+(-4-0)^{2}}=\sqrt{25+16}=\sqrt{41}$
