Question:
A tangent to the hyperbola $\frac{x^{2}}{4}-\frac{y^{2}}{2}=1$ meets $x$-axis at $P$ and $y$-axis at $Q$. Lines $P R$ and $Q R$ are drawn such that OPRQ is a rectangle (where $\mathrm{O}$ is the origin). Then $\mathrm{R}$ lies on :
Correct Option: , 2
Solution:
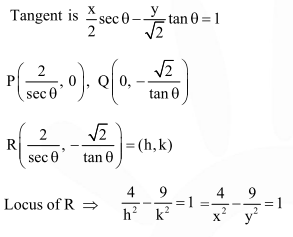
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
