A target shown in the given figure consists of three concentric circle of radii 3, 7 and 9 cm respectively. A dart is thrown and lands on the target. What is the probability that the dart will land on the shaded region?
Given: A target is shown in figure consists of three concentric circles of radius 3, 7, and 9 cm. A dart is thrown and lands on the target
To find: Probability that the dart will land in shaded region?
Total area of circle with radius 9 cm
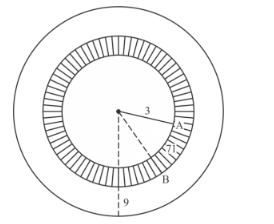
Area of circle with radius $9 \mathrm{~cm}=\pi r^{2}$
$=\pi(9)^{2}$
$=81 \pi \mathrm{cm}^{2}$
Area of shaded portion $=\pi\left(R^{2}-r^{2}\right)$
$=\pi\left(7^{2}-3^{2}\right)$
$=\pi(7+3)(7-3)$
$=\pi(10)(4)$
$=40 \pi$
We know that Probability $=\frac{\text { Number of favourable event }}{\text { Total number of event }}$
Hence probability of the spinner will land in shaded region is $\frac{40 \pi}{81 \pi}=\frac{40}{81}$
