A tent is in the form of a right circular cylinder surmounted by a cone.

We have a right circular cylinder surmounted by a cone.

Diameter of cylinder = 24 m, Height if cylindrical portion = 11 m and the vertex of the cone is 16 meters above the ground. We have to find the area of canvas required for the tent.

Suppose curved area of the cone portion is.

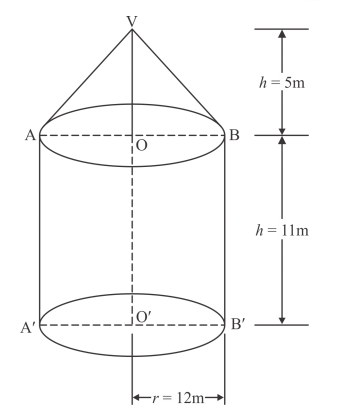
From the above figure the slant height of the top is given by

$l=\sqrt{5^{2}+12^{2}}$

$=13 \mathrm{~m}$

$r=\frac{24}{2}=12 \mathrm{~m}$

$S_{1}=\pi r l$

$=\frac{22}{7} \times 12 \times 13 \mathrm{~m}^{2}$

Now, Let us suppose that the curved area of cylinder is 

$S_{2}=2 \pi r h$

$=2 \times \frac{22}{7} \times 12 \times 11 \mathrm{~m}^{2}$

Therefore, the area of canvas is given by

$S=S_{1}+S_{2}$

$=\left(\frac{22}{7} \times 12 \times 13+2 \times \frac{22}{7} \times 12 \times 11\right) \mathrm{m}^{2}$

$=\frac{22}{7}(12 \times 13+2 \times 12 \times 11) \mathrm{m}^{2}$

$=\frac{22}{7} \times 420 \mathrm{~m}^{2}$

$=1320 \mathrm{~m}^{2}$

Hence, $S=1320 \mathrm{~m}^{2}$