A tower subtends an angle α at a point A in the plane of its base

Let  be the height of tower. The tower CD subtends an angle  at a point. And the angle of depression of foot of tower at a point b meter just above  is. Let  and, .

Here we have to prove height of tower is 

We have the corresponding figure as follows

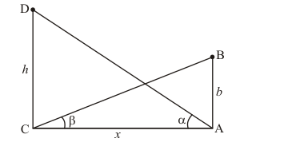
So we use trigonometric ratios.

In,

$\Rightarrow \quad \tan \beta=\frac{A B}{A C}$

$\Rightarrow \quad \tan \beta=\frac{b}{x}$

$\Rightarrow \quad x=\frac{b}{\tan \beta}$

$\Rightarrow \quad x=b \cot \beta$

Again in $\triangle A C D$

$\Rightarrow \quad \tan \alpha=\frac{C D}{A C}$

$\Rightarrow \quad \tan \alpha=\frac{h}{x}$

$\Rightarrow \quad h=x \tan \alpha$

$\Rightarrow \quad h=b \tan \alpha \cot \beta$

Hence the height of tower is $b \tan \alpha \cot \beta$.