A toy is in the form of a cone surmounted on a hemisphere.

Given that, a toy is in the form of a cone surmounted on the hemisphere.

Diameter of the base $d=6 \mathrm{~cm}$ and the height of the cone $h=4 \mathrm{~cm}$, then we have to find the surface area of the toy.

We have the following figure

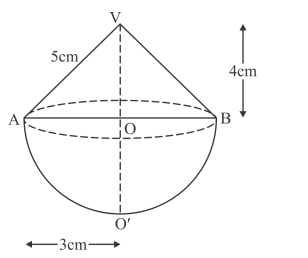
The radius of the base is

$r=\frac{d}{2}$

$=\frac{6}{2}=3 \mathrm{~cm}$

From the above figure, the slant height of the cone is

$l=\sqrt{r^{2}+h^{2}}$

$=\sqrt{3^{2}+4^{2}}$

$=5 \mathrm{~cm}$

We know that when the surface area of the cone is, then

$S_{1}=\pi r l$

$=3.14 \times 3 \times 5$

$=47.1 \mathrm{~cm}^{2}$

The surface area of the hemisphere is

$S_{2}=2 \pi r^{2}$

$=2 \times 3.14 \times 3^{2}$

$=56.52 \mathrm{~cm}^{2}$

Therefore the surface area of the toy is

$S=S_{1}+S_{2}$

$=47.1+56.52$

$=103.62 \mathrm{~cm}^{2}$

Hence, $S=103.62 \mathrm{~cm}^{2}$