A toy is in the shape of a right circular cylinder

Solution:

We have the following diagram

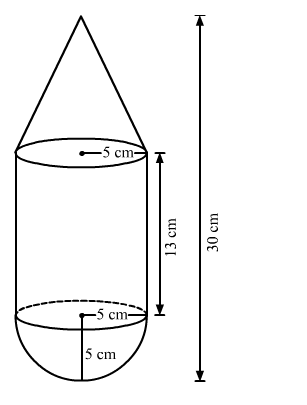
For cylindrical part, we have

$h=13 \mathrm{~cm}$

 

$r=5 \mathrm{~cm}$

Therefore, the curved surface area of the cylinder is given by

$S_{1}=2 \pi r h$

$=2 \times 3.14 \times 5 \times 13$

$=408.2 \mathrm{~cm}^{2}$

For conical part, we have

$h=30-13-5$

$=12 \mathrm{~cm}$

$l=\sqrt{h^{2}+r^{2}}$

$=13 \mathrm{~cm}$

Therefore, the curved surface area of the conical part is

$S_{2}=\pi r l$

$=3.14 \times 5 \times 13$

$=204.1 \mathrm{~cm}^{2}$

For hemisphere, we have

$r=5 \mathrm{~cm}$

Therefore the surface area of the hemisphere is

$S_{3}=2 \pi r^{2}$

$=2 \times 3.14 \times 5^{2}$

 

$=157 \mathrm{~cm}^{2}$

The total surface area of the toy is

$S=S_{1}+S_{2}+S_{3}$

$=408.2+204.1+157$

 

$=769.3 \mathrm{~cm}^{2}$

Hence, total surface area of the toy is $S=769.3 \mathrm{~cm}^{2}$