Question:
A uniform cylinder of mass $M$ and radius $R$ is to be pulled over a step of height $a(a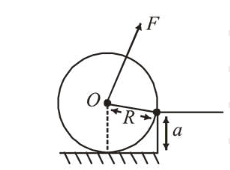
Correct Option: 1
Solution:
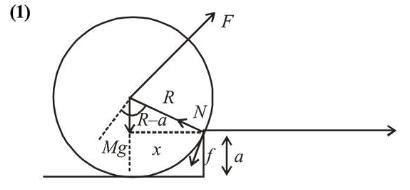
For step up, $F \times R \geq M g \times x$
$x=\sqrt{R^{2}-(R-a)^{2}}$ from figure
$F_{\min }=\frac{M g}{R} \times \sqrt{R^{2}-(R-a)^{2}}=M g \sqrt{1-\left(\frac{R-a}{R}\right)^{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.