A vertical pole 6 m long casts a shadow of length 3.6 m on the ground.

(d) 30 m

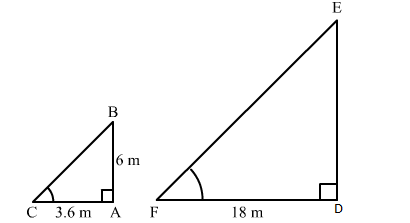
Let AB and AC be the vertical pole and its shadow, respectively.
According to the question:
AB = 6 m
AC = 3.6 m
Again, let DE and DF be the tower and its shadow.
According to the question:
DF = 18 m
​DE = ?
Now, in right-angled triangles ABC and DEF, we have:

$\angle B A C=\angle E D F=90^{\circ}$

$\angle A C B=\angle D F E \quad$ (Angular elevation of the Sun at the same time)

Therefore, by AA similarity theorem, we get:

$\triangle A B C \sim \triangle D E F$

$\Rightarrow \frac{A B}{A C}=\frac{D E}{D F}$

$\Rightarrow \frac{6}{3.6}=\frac{D E}{18}$

$\Rightarrow D E=\frac{6 \times 18}{36}=30 \mathrm{~m}$