A vertically straight tree, 15 m high, is broken by the wind in such a way that it top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
Let 
be the tree of desired height x m and tree is broken by wind then tree makes an angle 
. Let AC=15 − x
Here we have to find height x
So we use trigonometric ratios.
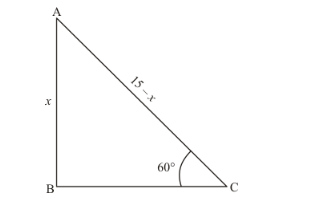
In a triangle
,
$\Rightarrow \quad \sin C=\frac{A B}{A C}$
$\Rightarrow \quad \sin 60^{\circ}=\frac{x}{15-x}$
$\Rightarrow \quad \frac{\sqrt{3}}{2}=\frac{x}{15-x}$
$\Rightarrow 15 \sqrt{3}-\sqrt{3} x=2 x$
$\Rightarrow \quad 15 \sqrt{3}=2 x+\sqrt{3} x$
$\Rightarrow \quad 15 \sqrt{3}=x(2+\sqrt{3})$
$\Rightarrow \quad x=\frac{15 \sqrt{3}}{2+\sqrt{3}}$
$\Rightarrow \quad x=6.9$
Hence the height of tree is $6.9 \mathrm{~m}$.