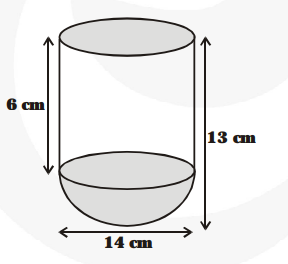
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder.

For hemispherical part, radius (r) $=\frac{\mathbf{1 4}}{\mathbf{2}}=7 \mathrm{~cm}$

$\therefore \quad$ Curved surface area $=2 \pi \mathrm{r}^{2}$

$=2 \times \frac{22}{7} \times 7 \times 7 \mathrm{~cm}^{2}=308 \mathrm{~cm}^{2}$

Total height of vessel $=13 \mathrm{~cm}$

$\therefore$ Height of cylinder $=(13-7) \mathrm{cm}=6 \mathrm{~cm}$ and radius $(\mathrm{r})=7 \mathrm{~cm}$

$\therefore \quad$ Curved surface area of cylinder $=2 \pi \mathrm{rh}$

$=2 \times \frac{\mathbf{2 2}}{\mathbf{7}} \times 7 \times 6 \mathrm{~cm}^{2}=264 \mathrm{~cm}^{2}$

$\therefore \quad$ Inner surface area of vessel $=$ Curved surface area of hemispherical part $+$ Curved surface area of cylinder

$=(308+264) \mathrm{cm}^{2}=572 \mathrm{~cm}^{2}$