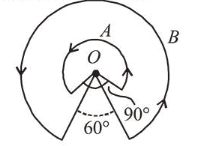
A wire $A$, bent in the shape of an arc of a circle, carrying a current of 2 A and having radius $2 \mathrm{~cm}$ and another wire $B$, also bent in the shape of arc of a circle, carrying a current of $3 \mathrm{~A}$ and having radius of $4 \mathrm{~cm}$, are placed as shown in the figure. The ratio of the magnetic fields due to the wires $A$ and $B$ at the common centre $O$ is :
Correct Option: , 4
(4) Given : $I_{A}=2 \mathrm{~A}, R_{A}=2 \mathrm{~cm}, \theta_{A}=2 \pi-\frac{\pi}{2}=\frac{3 \pi}{2}$
$I_{B}=3 \mathrm{~A}, R_{B}=4 \mathrm{~cm}, \theta_{B}=2 \pi-\frac{\pi}{3}=\frac{5 \pi}{3}$
Using, magnetic field, $B=\frac{\mu_{0} I \theta}{4 \pi R}$
$\frac{B_{A}}{B_{B}}=\frac{I_{A}}{I_{B}} \times \frac{\theta_{A} R_{B}}{\theta_{B} R_{A}}=\frac{2 \times \frac{3 \pi}{2} \times 4}{3 \times \frac{5 \pi}{3} \times 2}=\frac{6}{5}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
