Question:
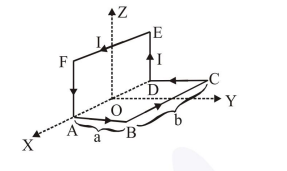
A wire carrying current $I$ is bent in the shape ABCDEFA as shown, where rectangle ABCDA and ADEFA are perpendicular to each other. If the sides of the rectangles are of lengths a and $b$, then the magnitude and direction of magnetic moment of the loop $\mathrm{ABCDEFA}$ is :
Correct Option: 1
Solution:
$\mathrm{M}=\mathrm{NIA}$
$\mathrm{N}=1$
For $\mathrm{ABCD}$
$\overrightarrow{\mathrm{M}}_{1}=\mathrm{abI} \hat{\mathrm{K}}$
For DEFA
$\overrightarrow{\mathrm{M}}_{2}=\mathrm{abI} \hat{\mathrm{j}}$
$\overrightarrow{\mathrm{M}}=\overrightarrow{\mathrm{M}}_{1}+\overrightarrow{\mathrm{M}}_{2}$
$=a b I(\hat{k}+\hat{j})$
$=a b I \sqrt{2}\left(\frac{\hat{j}}{\sqrt{2}}+\frac{\hat{k}}{\sqrt{2}}\right)$
