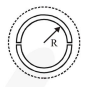
A wooden wheel of radius $\mathrm{R}$ is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross sectional area $\mathrm{S}$ and Length $\mathrm{L}$. $\mathrm{L}$ is slightly less than $2 \pi \mathrm{R}$. To fit the ring on the wheel, it is heated so that its temperature rises by $\Delta \mathrm{T}$ and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is $\alpha$, and its Young's modulus is Y, the force that one part of the wheel applies on the other part is :
Correct Option: 1
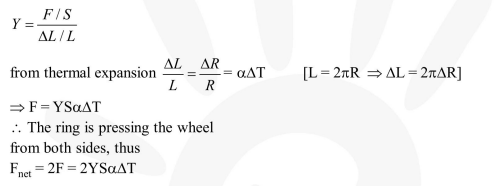
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
