AB and CD are respectively the smallest and largest sides of a quadrilateral ABCD

Solution:

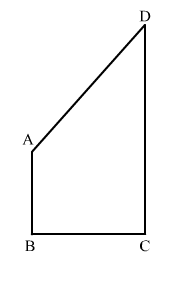
Given: In quadrilateral ABCD, AB and CD are respectively the smallest and largest sides.

To prove:
​(i) ∠A > ∠C
(ii) ∠B > ∠D

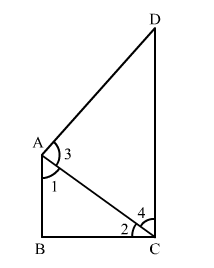
Construction: Join AC.

Proof:

In $\Delta A B C$,

$\because B C>A B \quad$ (Given, $A B$ is the smallest side)

$\therefore \angle 1>\angle 2 \quad \ldots(1)$

In $\Delta A D C$,

$\because C D>A D \quad$ (Given, $C D$ is the largest side)

$\therefore \angle 3>\angle 4 \quad \ldots(2)$

Adding (1) and (2), we get

$\angle 1+\angle 3>\angle 2+\angle 4$

$\therefore \angle A>\angle C$

(ii)

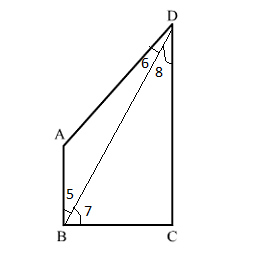
Construction: Join BD.

Proof:

In $\Delta A B D$,

$\because A D>A B \quad$ (Given, $A B$ is the smallest side.)

$\therefore \angle 5>\angle 6 \quad \ldots(3)$

In $\Delta C B D$,

$\because C D>B C \quad$ (Given, $C D$ is the greatest side.)

$\therefore \angle 7>\angle 8 \quad \ldots(4)$

Adding $(3)$ and $(4)$, we get

$\angle 5+\angle 7>\angle 6+\angle 8$

$\therefore \angle B>\angle D$