Question:
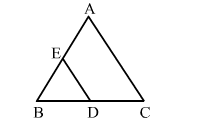
∆ABC and ∆BDE are two equilateral triangles such that D is the midpoint of BC. Then, ar(∆BDE) : ar(∆ABC) = ?
(a) $1: 2$
(b) $1: 4$
(c) $\sqrt{3}: 2$
(d) $3: 4$
Solution:
(b) 1:4
∆ABC and ∆BDE are two equilateral triangles and D is the midpoint of BC.
Let AB = BC = AC = a
Then $\mathrm{BD}=B E=E D=\frac{a}{2}$
$\therefore \frac{\operatorname{ar}(\Delta B D E)}{\operatorname{ar}(\Delta A B C)}=\frac{\frac{\sqrt{3}}{4} A B^{2}}{\frac{\sqrt{3}}{4} B E^{2}}=\frac{\left(\frac{a}{2}\right)^{2}}{a^{2}}=\frac{1}{4}$
So, required ratio $=1: 4$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.