ABC is a right angled triangle, right angled at B such that BC = 6 cm and AB = 8 cm.

Let us first put the given data in the form of a diagram.

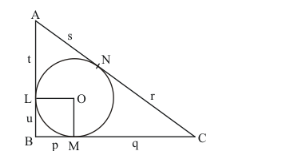
Let us first find out AC using Pythagoras theorem.

$A C^{2}=A B^{2}+B C^{2}$

$A C^{2}=8^{2}+6^{2}$

$A C^{2}=64+36$

$A C^{2}=100$

$A C=10$

Also, we know that tangents drawn from an external point will be equal in length. Therefore we have the following,

BL = BM …… (1)

CM = CN …… (2)

AL = AN …… (3)

We have found that,

AC = 10

That is,

AN + NC = 10

But from (2) and (3), we can say

AL + MC = 10 …… (4)

It is given that,

AB = 8

BC = 6

Therefore,

AB + BC =14

Looking at the figure, we can rewrite this as,

AL + LB + BM + MC = 14

(AL + MC) + (BM + BL) = 14

Using (1) and (3) we can write the above equation as,

10 + 2BL = 14

BL = 2Consider the quadrilateral, BLOM, we have,

BL = BM (From (1))

OL = OM(Radii of the same circle)

$\angle L B M=90^{\circ}$ (Given data)

$\angle B L O=90^{\circ}$ (Radii is always perpendicular to the tangent at the point of contact)

$\angle B M O=90^{\circ}$ (Radii is always perpendicular to the tangent at the point of contact)

Since the sum of all angles of a quadrilateral will be equal to , we have,

$\angle L B M+\angle L O M+\angle B L O+\angle B M O=360^{\circ}$

$90^{\circ}+90^{\circ}+90^{\circ}+\angle L O M=360^{\circ}$

$\angle L O M=90^{\prime}$

Since all the angles of the quadrilateral are equal to  and since adjacent sides are equal, the quadrilateral BLOM is a square. We know that all the sides of a square are of equal length.

We have found BL = 2

Therefore,

OM = 2

OM is nothing but the radius of the circle.

Therefore, radius of the circle is 2 cm.

Hence the correct answer to the question is option (b).