Question:
∆ABC is right-angled at A and AD ⊥ BC. If BC = 13 cm and AC = 5 cm, find the ratio of the areas of ∆ABC and ∆ADC.
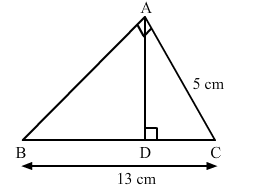
Solution:
In $\triangle A B C$ and $\triangle A D C$, we have:
$\angle B A C=\angle A D C=90^{\circ}$
$\angle A C B=\angle A C D \quad$ (common)
By AA similarity, we can conclude that $\triangle B A C \sim \triangle A D C$.
Hence, the ratio of the areas of these triangles is equal to the ratio of squares of their corresponding sides.
$\therefore \frac{\operatorname{ar}(\Delta B A C)}{\operatorname{ar}(\Delta A D C)}=\frac{B C^{2}}{A C^{2}}$
$\Rightarrow \frac{\operatorname{ar}(\Delta B A C)}{\operatorname{ar}(\Delta A D C)}=\frac{13^{2}}{5^{2}}$
$=\frac{169}{25}$
Hence, the ratio of areas of both the triangles is 169 : 25
