ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F
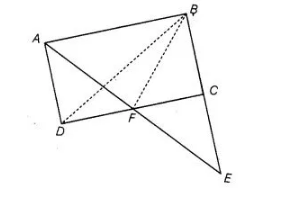
If ar (ΔDFB) = 3 cm2, then find the area of the parallelogram ABCD.
Given, $A B C D$ is a parallelogram and $C E=B C$ i.e., $C$ is the mid-point of $B E$.
Also, $\operatorname{ar}(\Delta D F B)=3 \mathrm{~cm}^{2}$
Now, $\triangle A D F$ and $\triangle D F B$ are on the same base $D F$ and between parallels $C D$ and $A B$. Then,
ar $(\triangle A D F)=\operatorname{ar}(\triangle D F B)=3 \mathrm{~cm}^{2}$ ...(i)
In $\triangle A B E$, by the converse of mid-point theorem,
$E F=A F$ [since, $C$ is mid-point of $B E] \ldots$ (ii)
In $\triangle A D F$ and $\triangle E C F$.
$\angle A F D=\angle C F E$ [vertically opposite angles]
$A F=E F$ [from Eq. (ii)]
and $\angle D A F=\angle C E F$
[since, $B E \| A D$ and $A E$ is transversal, then alternate interior angles are equal]
$\therefore \quad \triangle A D F \equiv \triangle F C F \quad$ [by ASA congruence rule]
Then, $\operatorname{ar}(\triangle A D F)=\operatorname{ar}(\triangle C F E)$
[since, congruent figures have equal area]
$\therefore \quad \operatorname{ar}(\Delta C F E)=\operatorname{ar}(\triangle A D F)=3 \mathrm{~cm}^{2} \quad$ [from Eq. (i)]...(iii)
Now, in $\triangle B F E, C$ is the mid-point of $B E$ then $C F$ is median of
$\triangle B F E$
$\therefore \quad a r(\Delta C E F)=\operatorname{ar}(\triangle B F C)$
[since, median of a triangle divides it into two triangles of equal area]
$\Rightarrow \quad$ ar $(\Delta B F C)=3 \mathrm{~cm}^{2}$ ...(iv)
Now, $\quad \operatorname{ar}(\Delta B D C)=\operatorname{ar}(\Delta D F B)+\operatorname{ar}(\Delta B F C)$
$=3+3=6 \mathrm{~cm}^{2}$ [from Eqs. (i) and (iv)]
We know that, diagonal of a parallelogram divides it into two congruent triangles of equal areas.
$\therefore \quad$ Area of parallelogram $A B C D=2 \times$ Area of $\triangle B D C$
$=2 \times 6=12 \mathrm{~cm}^{2}$
Hence, the area of parallelogram $A B C D$ is $12 \mathrm{~cm}^{2}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
