Question:
ABCD is a quadrilateral in which AD = BC. If P, Q, R , S be the mid points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
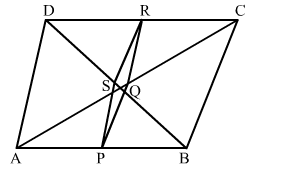
Solution:
In △ABC, P and Q are mid points of AB and AC respectively.
So, $\mathrm{PQ} \| \mathrm{BC}$, and $\mathrm{PQ}=\frac{1}{2} \mathrm{BC}$ ..........(1)
Similarly, In $\triangle \mathrm{ADC}, \mathrm{QR}=\frac{1}{2} \mathrm{AD}=\frac{1}{2} \mathrm{BC}$ ............(2)
Now, In $\triangle \mathrm{BCD}, \mathrm{SR}=\frac{1}{2} \mathrm{BC}$ ........(3)
Similarly, In $\triangle \mathrm{ABD}, \mathrm{PS}=\frac{1}{2} \mathrm{AD}=\frac{1}{2} \mathrm{BC}$ .............(4)
Using (1), (2), (3) and (4)
PQ = QR = SR = PS
Since, all sides are equal
Hence, PQRS is a rhombus.
