ABCD is a quadrilateral such that A is the centre of the circle passing through B, C and D.

In the given figure, ABCD is a quadrilateral such that A is the centre of the circle passing through B, C and D.

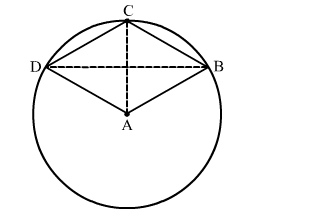
Join AC and BD.

We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it on the remaining part of the circle.

Here, arc CD subtends ∠CAD at the centre and ∠CBD at B on the circle.

∴ ∠CAD = 2∠CBD           ...(1)

Also, arc CB subtends ∠CAB at the centre and ∠CDB at D on the circle.

∴ ∠CAB = 2∠CDB           ...(2)

Adding (1) and (2), we get
∠CAD + ∠CAB = 2(∠CBD + ∠CDB)
⇒ ∠BAD = 2(∠CBD + ∠CDB)

$\Rightarrow \angle C B D+\angle C D B=\frac{1}{2} \angle B A D$

Hence, $\angle C B D+\angle C D B=\frac{1}{2} \angle B A D$.