ABCD is a rectangle.

Given: ABCD is a cyclic rectangle whose diagonals intersect at O.
To prove: O is the centre of the circle.
Proof:

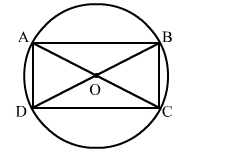
Here, ∠BCD = 90°     [Since it is a rectangle]
So, BD is the diameter of the circle (if the angle made by the chord at the circle is right angle, then the chord is the diameter).
Also, diagonals of a rectangle bisect each other and are equal.
∴ OA =  OB = OC = OD
BD is the diameter.
∴ BO and OD are the radius.
Thus, O is the centre of the circle.
Also, the centre of the circle is circumscribing the cyclic rectangle.
Hence, O is the point of intersection of the diagonals of ABCD.